近日，《物理评论快报》(Physical Review Letters)在线发表了数学与统计学院教授周进课题组关于复杂网络中圈结构重要性识别的研究进展。

论文题目为“Searching for Key Cycles in a Complex Network”（《寻找复杂网络中的关键圈》）。武汉大学为论文的第一署名单位，数学与统计学院周进教授为通讯作者，数学与统计学院2021级硕博连读研究生蒋思杨为论文第一作者，合作者包括数学与统计学院陆君安教授、硕士研究生张妍琪以及西澳大学Michael Small教授。

此项研究首次指出了网络圈的重要性与图的Fiedler向量的定量关系。研究人员找到一个简单的公式评估任一个圈对网络动力学(同步、扩散、一致性、控制等)的贡献，该公式只需要Fiedler向量的分量。该研究首先指出Fiedler值(Laplacian矩阵的次小特征值)是网络一致性动力学中的重要指标，圈结构对于一致性动力学起关键作用；并提出网络中圈的重要性排序理论，表明圈的重要性受圈的长度及在网络中位置的影响，有趣地发现位置好的小圈会比某些大圈更重要；将圈排序结果应用于边自适应牵制控制同步，发现排序算法简洁且高效；进一步将排序算法在线虫新陈代谢网络上加以应用。

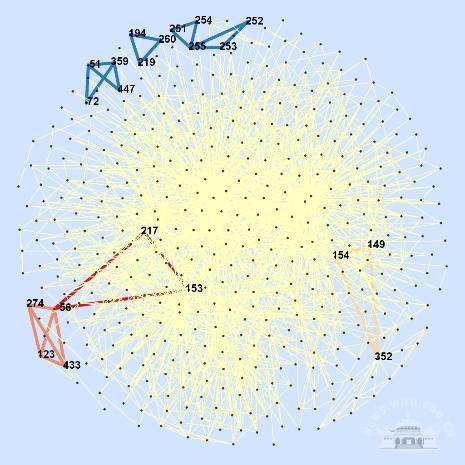
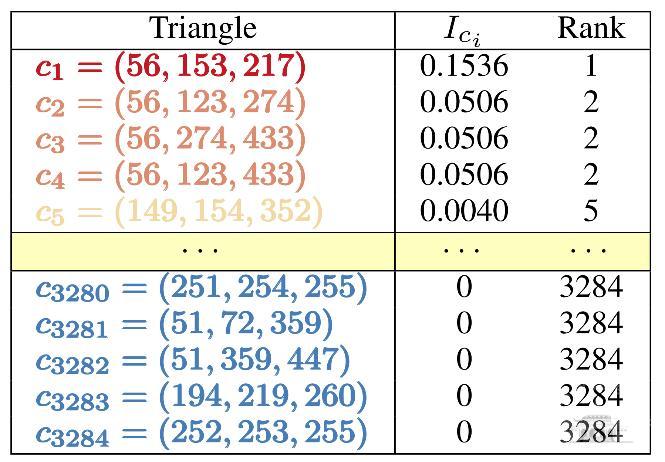
图 线虫新陈代谢网络的三角形分布情况

该工作阐述了圈结构对网络动力学行为的贡献，在复杂系统研究领域具有重要的意义，有望在网络的鲁棒性、脆弱性及网络攻击和防御中得到进一步应用。

周进教授所在的数学与统计学院复杂网络团队近年来一直致力于研究复杂系统的动力学，包括复杂网络同步、控制、传播、重要性结构识别以及多层网络和高阶网络的动力学，取得了很多突破性成果。该团队曾获2008年和2016年国家自然科学二等奖、2007年教育部自然科学一等奖、2013年和2006年湖北省自然科学一等奖和二等奖。

该研究得到了国家自然科学基金委员会的支持。

论文链接：https://link.aps.org/doi/10.1103/PhysRevLett.130.187402

（ 来源：数学与统计学院 ）